Далее: Вычисление константы скорости вырожденного Уровень выше: Вычисление константы скорости вырожденного Назад: Вычисление константы скорости вырожденного
При отсутствии кросс-релаксации (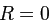 ) возможны дальнейшие упрощения:
) возможны дальнейшие упрощения:
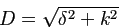
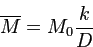
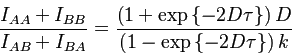
В случае равенства скоростей спин-решеточной релаксации в состояниях
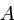 и
и 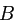 (
(
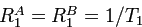
![]() , откуда следует
, откуда следует 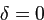 ,
,
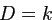 ,
,
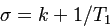
![]() ,
, 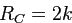
![]() ,
,
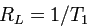
![]() ,
,
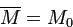
![]() ),
получаем упрощенное выражение:
),
получаем упрощенное выражение:
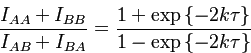
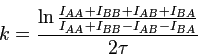
Если скорости спин-решеточной релаксации существенно различаются (
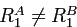
![]() ),
предлагается действовать следующим образом. Сначала по предыдущему
уравнению вычислить приближенное значение
),
предлагается действовать следующим образом. Сначала по предыдущему
уравнению вычислить приближенное значение 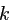 , из которого найти
начальное приближение для
, из которого найти
начальное приближение для 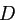 . Затем, сделав подстановку
. Затем, сделав подстановку
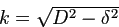
![]() и использовав указанное начальное приближение, численно решить относительно
и использовав указанное начальное приближение, численно решить относительно
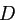 следующее уравнение:
следующее уравнение:
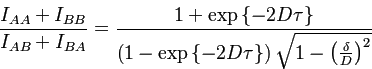
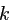 .
.
Георгий Сальников, sge@nmr.nioch.nsc.ru